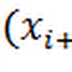Développement limité et parité
Si une fonction paire
(respectivement impaire) admet un DL au voisinage de 0, alors ce DL est paire
(respectivement impaire).
Démonstration :
On a : f(x) = a0
+ … + anxn + o(xn), avec n un entier.
·
Si f est paire ⇒ f(x) =
f(-x).
⇒ a0 + a1x + a2x2 + … + anxn = a0 - a1x + a2x2 + … + (-1)nanxn.
Alors :
a1 = - a1 ⇒ a1 = 0.
…
an = - an si n est impaire ⇒ an = 0 si n est impaire.
⇒ On conclut que tous les coefficients d’indice impaire sont nuls.
⇒ Le DL de f au voisinage de 0 est paire.
⇒ a0 + a1x + a2x2 + … + anxn = a0 - a1x + a2x2 + … + (-1)nanxn.
Alors :
a1 = - a1 ⇒ a1 = 0.
…
an = - an si n est impaire ⇒ an = 0 si n est impaire.
⇒ On conclut que tous les coefficients d’indice impaire sont nuls.
⇒ Le DL de f au voisinage de 0 est paire.
·
Si f est impaire
⇒ f(x) = -f(-x).
⇒ a0 + a1x + a2x2 + … + anxn = -a0 + a1x - a2x2 + … - (-1)nanxn.
Alors :
a0 = - a0 ⇒ a0 = 0.
…
an = - an si n est paire ⇒ an = 0 si n est paire.
⇒ On conclut que tous les coefficients d’indice paire sont nuls.
⇒ Le DL de f au voisinage de 0 est impaire.
⇒ a0 + a1x + a2x2 + … + anxn = -a0 + a1x - a2x2 + … - (-1)nanxn.
Alors :
a0 = - a0 ⇒ a0 = 0.
…
an = - an si n est paire ⇒ an = 0 si n est paire.
⇒ On conclut que tous les coefficients d’indice paire sont nuls.
⇒ Le DL de f au voisinage de 0 est impaire.
Exemple :
·
cos(x) est
paire.
cos(x) = 1 – x²/2 + … + (-1)n/2.(xn/n !) + o(xn) est le DLn de cos(x) au voisinage de 0.
Ce DL est paire.
cos(x) = 1 – x²/2 + … + (-1)n/2.(xn/n !) + o(xn) est le DLn de cos(x) au voisinage de 0.
Ce DL est paire.
·
sin (x) est impaire.
cos(x) = x – x3/2 + … + (-1)(n-1)/2.(xn/n !) + o(xn) est le DLn de sin(x) au voisinage de 0.
Ce DL est impaire.
cos(x) = x – x3/2 + … + (-1)(n-1)/2.(xn/n !) + o(xn) est le DLn de sin(x) au voisinage de 0.
Ce DL est impaire.
Formule de Taylor-Young
Soit f une
fonction de I dans R et a ∈ I. On dit que f admet un développement
limité d’ordre n (entier) en a (noté DLn) si : f(x) = f(a) + (x
– a).f’(a) + ((x – a)²/2).f’’(a) + … + ((x – a)n/n !).f(n)(a)
+ o(xn) = .
On Remarque que, si
on pose x = a + h ⇒ h = x - a alors :
On a :
⇒ ∀ 0≤i≤n ai = bi.
f(x) = f(a+h) = f(a) + h.f’(a) + (h²/2).f’’(a)
+ … + (hn/n !).f(n)(a) + o(hn) =
Si f admet un dévloppement
limité en a alors ce développement est unique.
Démonstration :
f peut s’écrire
sous la forme : f(x) =
.
On suppose que f(x)
= R(x) + o(xn) = Q(x) + o(xn). avec:
On a :
a1 = f(a)
= b1
…
⇒ ∀ 0≤i≤n ai = bi.
⇒ R(x) = Q(x).
⇒ Si f admet un développement limité en a
alors ce DL est unique.
Exemple :
Soit f(x) = ln(1 +
x).
On cherche le développent
limité de f en 1 à l’ordre 4.
ln(1 + x) = ln(1) + (1/a).x + (-1/a²).(x²/2)
+ (2/a3).(x3/6) + (-6/a4).(x4/24) +
o(x4)
= x + x²/2 – x3/3 + x4/4
+ o(x4).
Comment tracer une fonction en escalier avec Sine Qua non
1.
Lancer le
logiciel.
2. Cliquer sur «Définir une fonction ».
3. Dans la case de « f1 (x) »
ecrir : « int(x) » puis « ok ».
4. Et voila :
Application en escalier
Une application e : [a ;b] → ℝ est
dite en escalier s’il existe une subdivision s = (a1 ; … ;
an) de [a ;b], tel que n≥1 (entier), et (λ1 ;
… ; λn) tel que, ∀ 0 ≤ i ≤ n-1 , ∀ x ∈ ]ai ;
ai+1[, e(x) = λi.
On note E(a ;b) l’ensemble des application en
escalier de [a ;b].
On dit que s est une subdivision adapté à e.
Exemple :
Soit la fonction en escalier f(x) = E(x) ∀ x ∈
[-2 ; 2].
Propriétés :
1. Si e ∈ E(a ;b) alors ∃ une
subdivision de [a ;b] adapté à e.
2. Si s est adapté à e alors toute subdivision plus fine que
s est aussi adapté à e.
3. L’ensemble de subdivision adapté à e ∈
E(a ;b) admet un plus petit élément (pour l’ordre < dans l’ensemble de
subdivision de [a ;b]), qui est la subdivision formée par a, b et les
point de discontinuité de e.
4. 1 ∈ E(a ;b).
5. ∀ (e1 ;e2) ∈ (E(a ;b))2, on a : e1
+ e2 ∈ E(a ;b) et e1e2
∈ E(a ;b).
6. ∀ e ∈ E(a ;b), |e| ∈ E(a ;b).
Demonstration:
1. Par definition: Une application e : [a ;b] → ℝ est
dite en escalier s’il existe une subdivision s = (a1 ; … ;
an) de [a ;b], tel que n≥1 (entier), et (λ1 ;
… ; λn) tel que, ∀ 0 ≤ i ≤ n-1 , ∀ x ∈ ]ai ;
ai+1[, e(x) = λi.
2. s = (a1 ; … ; an) est
adapté à e ⇒ ∃ (λ1 ; … ; λn), avec
n≥1 (entier), tel que ∀ 0 ≤ i ≤ n-1 , ∀ x ∈ ]ai ;
ai+1[, e(x) = λi.
soit s’ = (a1 ; … ; ak ; c ; ak+1 ; … ; an) plus fine que s, avec 0 ≤ k ≤ n-1. Or ∀ 0 ≤ i ≤ n-1 , ∀ x ∈ ]ai ; ai+1[, e(x) = λi ⇒ ∀ x ∈ ]ak ; ak+1[, e(x) = λk ⇒ ∀ x ∈ ]ak ; c[, e(x) = λk et ∀ x ∈ ]c ; ak+1 [, e(x) = λk ⇒ s’ est adapté à e.
soit s’ = (a1 ; … ; ak ; c ; ak+1 ; … ; an) plus fine que s, avec 0 ≤ k ≤ n-1. Or ∀ 0 ≤ i ≤ n-1 , ∀ x ∈ ]ai ; ai+1[, e(x) = λi ⇒ ∀ x ∈ ]ak ; ak+1[, e(x) = λk ⇒ ∀ x ∈ ]ak ; c[, e(x) = λk et ∀ x ∈ ]c ; ak+1 [, e(x) = λk ⇒ s’ est adapté à e.
3. On raisonne par l’absurde :
On suppose que ∃ une subdivision adaptée à e, qui est plus petit que la subdivision formée par a, b et les point de discountés de e ⇒ ∃ i ∈ {1 ; … ; n-1} tel que ∀ x ∈ ]ai-1 ; ai+1[, e(x) = c ∈ ℝ. Or e n’est pas continue en ai donc e n’est pas constante sur ]ai-1 ; ai+1[ ⇒ absurdité.
Conclusion : L’ensemble de subdivision adapté à e ∈ E(a ;b) admet un plus petit élément (pour l’ordre < dans l’ensemble de subdivision de [a ;b]), qui est la subdivision formée par a, b et les point de discontinuité de e.
On suppose que ∃ une subdivision adaptée à e, qui est plus petit que la subdivision formée par a, b et les point de discountés de e ⇒ ∃ i ∈ {1 ; … ; n-1} tel que ∀ x ∈ ]ai-1 ; ai+1[, e(x) = c ∈ ℝ. Or e n’est pas continue en ai donc e n’est pas constante sur ]ai-1 ; ai+1[ ⇒ absurdité.
Conclusion : L’ensemble de subdivision adapté à e ∈ E(a ;b) admet un plus petit élément (pour l’ordre < dans l’ensemble de subdivision de [a ;b]), qui est la subdivision formée par a, b et les point de discontinuité de e.
4. f(x) = 1, ∀ x ∈ [a ; b], est une fonction constante donc f est
une fonction en escalier car ∀ x ∈ [a ; b], f(x) = 1.
5. Soit s’ la subdivision adapté à e1 et s’’ la
subdivision adapté à e2.
s’ = (a = a1 ; … ; an1 = b).
∀ 0≤ i ≤ n1-1, ∀ x ∈ ] ai ; ai+1[,e1(x) = αi
s’’ = (a = b1 ; … ; bn2 = b).
∀ 0≤ i ≤ n2-1, ∀ x ∈ ] bi ; bi+1[,e2(x) = βi
s = s’ ⋁ s’’.
s = (a = c1 ; … ; cn = b).
s est plus fine que s’ et s” donc s est une subdivision adaptée à e1 et e2.
∀ 0≤ i ≤ n-1, ∀ x ∈ ] ci ; ci+1[, e1(x) = θi et e2(x) = ωi.
⇒ ∀ 0≤ i ≤ n-1, ∀ x ∈ ] ci ; ci+1[, (e1 + e2)(x) = θi + ωi = νi.
⇒ e1 + e2 est une fonction en escalier ⇒ e1 + e2 ∈ E(a ; b) et s est la subdivision adaptée à e.
D’autre part, ∀ 0≤ i ≤ n-1, ∀ x ∈ ] ci ; ci+1[, e1e2(x) = θiωi = ψi.
⇒ e1e2 est une fonction en escalier ⇒ e1e2 ∈ E(a ; b) et s est la subdivision adaptée à e.
s’ = (a = a1 ; … ; an1 = b).
∀ 0≤ i ≤ n1-1, ∀ x ∈ ] ai ; ai+1[,e1(x) = αi
s’’ = (a = b1 ; … ; bn2 = b).
∀ 0≤ i ≤ n2-1, ∀ x ∈ ] bi ; bi+1[,e2(x) = βi
s = s’ ⋁ s’’.
s = (a = c1 ; … ; cn = b).
s est plus fine que s’ et s” donc s est une subdivision adaptée à e1 et e2.
∀ 0≤ i ≤ n-1, ∀ x ∈ ] ci ; ci+1[, e1(x) = θi et e2(x) = ωi.
⇒ ∀ 0≤ i ≤ n-1, ∀ x ∈ ] ci ; ci+1[, (e1 + e2)(x) = θi + ωi = νi.
⇒ e1 + e2 est une fonction en escalier ⇒ e1 + e2 ∈ E(a ; b) et s est la subdivision adaptée à e.
D’autre part, ∀ 0≤ i ≤ n-1, ∀ x ∈ ] ci ; ci+1[, e1e2(x) = θiωi = ψi.
⇒ e1e2 est une fonction en escalier ⇒ e1e2 ∈ E(a ; b) et s est la subdivision adaptée à e.
6. Soit s la subdivion adaptée à e, avec s = (a = a1 ;
… ; an1 = b).
∀ 0≤ i ≤ n-1, ∀ x ∈ ] ai ; ai+1[, e(x) = λi.
⇒ ∀ 0≤ i ≤ n-1, ∀ x ∈ ] ai ; ai+1[, |e|(x) = |λi|.
⇒ |e| ∈ E(a ; b) et s est la subdivision adaptée à |e|.
∀ 0≤ i ≤ n-1, ∀ x ∈ ] ai ; ai+1[, e(x) = λi.
⇒ ∀ 0≤ i ≤ n-1, ∀ x ∈ ] ai ; ai+1[, |e|(x) = |λi|.
⇒ |e| ∈ E(a ; b) et s est la subdivision adaptée à |e|.
Exemple :
1. Soit f(x) = E(x), ∀ x ∈
[-2 ; 2].
s = (-2 ; -1 ; 0 ; 1 ; 2) est une subdivision adaptée à f.
s = (-2 ; -1 ; 0 ; 1 ; 2) est une subdivision adaptée à f.
2. Prenons l’exemple (1) : s’ = (-2 ; -1 ;
0 ; 0,5 ; 1 ; 2) est plus fine que s. s’ est une subdivision
adaptée à f.
3. Prenons le même exemple : s = (-2 ; -1 ;
0 ; 1 ; 2) est la subdivision la plus petite ((pour l’ordre < dans
l’ensemble de subdivision de [-2 ;2]), qui est adaptée à f.
4. f(x) = 1, ∀ x ∈ [-2 ;2] est une fonction en escalier.
5. Soit f(x) = E(x) et g(x) = E(x) – 1 , ∀ x ∈
[-2 ;2].
(f+g)(x) = 2E(x) -1 est une fonction en escalier.
fg(x) = E²(x) – E(x) est une fonction en escalier.
(f+g)(x) = 2E(x) -1 est une fonction en escalier.
fg(x) = E²(x) – E(x) est une fonction en escalier.
6. Soit f(x) = E(x), ∀ x ∈
[-2 ;2].
|f|(x) = E(x), ∀ x ∈ [-2 ;2].
|f| est une fonction en escalier.
|f|(x) = E(x), ∀ x ∈ [-2 ;2].
|f| est une fonction en escalier.
Subdivision
Une subdivision (ou partage) de
[a ;b], tel que a<b, est une famille (xi)0≤i≤n ,
avec n≥1 (entier), tel que a=x1<…<xn=b.
Exemple :
Soit l’intervalle [1 ;5].
{1 ; 2
;3,5 ;4 ;4,68 ;5} est une subdivision de [1 ;5].
Le pas :
On note, d’abord, S l’ensemble de
subdivision de [a ;b].
Soit s = (xi)0≤i≤n
∈ S, avec
n≥1 (entier).
Exemple :
Prenons le dernier exemple :
Soit s = { x1
= 1; x2 = 2; x3 = 3,5; x4 = 4; x5 =
4,68 et x6 = 5}.
p(s)=
= x2 - x1
= 2 – 1 = 1.
Relation d’ordre et
lois internes:
∀
(s,s’) ∈ S, s<s’ ⇔ s’ est plus fine que s.
S est muni de deux lois internes qui sont ⋁
et ⋀.
Démonstration :
Soit F l’ensemble des parties
finies de [a ;b] contenants a et b, et soit S.
θ : S → F est une bijection
car chaque subdivision (xi)0≤i≤n de [a ;b], avec n≥1
(entier), est associé à un ensemble {a=x1 ; … ; xn=b}
∈ F.
Or F est naturellement muni par
la relation d’ordre définie par l’inclusion et stable par la réunion et
l’intersection.
La bijection de θ permet de
transporter l’inclusion et les loi internes (⋃, ⋂) de F dans S.
Donc :
·
θ (s) ⊂ θ (s’) ⇔ s < s’.
·
θ -1(θ (s)
⋃ θ (s’)) ⇔ s ⋁ s’.
·
θ -1(θ (s)
⋂ θ (s’)) ⇔ s ⋀ s’.
Exemple :
Soit
deux subdivisions de [0 ;1].
On a :
·
s < s’.
·
s ⋁ s’ =
·
s ⋀ s’ =
D’autre part si
on ne peut pas comparer s et s’ par <.La différence entre un ensemble et une famille
Un ensemble est
une collection ou un groupement d’objets distincts, appelés éléments de cet
ensemble.
Exemple :
E = {a ;b ;c ;d}
E est un ensemble
de 4 éléments.
a, b, c et d sont
les éléments de E.
D’autre part, une
famille est une application, d’un ensemble I d’indices vers un autre ensemble,
qui à tout élément i ∈ I associait un élément, de l’ensemble d’arrivé,
noté xi et prononcé x d’indice i.
La différence
entre l’ensemble image {x tel que ∃ i ∈ I, x = xi} et un ensemble est que
dans ce dernier, on ne répète pas les éléments, alors que dans la famille (xi)i
∈ I, il peut y avoir plusieurs fois le même élément
si l’application n’est pas injective.
Exemple :
(xi)i
∈ I est une famille de 4 éléments qui sont x1,
x2, x3 et x4.
Cet famille est une application de {1 ;2 ;3 ;4} vers { x1 ;x2;x3;x4}.
Inscription à :
Articles (Atom)